Descriptive Stats & Distributions

http://tinyurl.com/4dfuycvt

Camilo G.

ca.garcia2@uniandes.edu.co

Alejandra S.

m.soto2@uniandes.edu.co

Ronald D.

r.diazf@uniandes.edu.co

Andrew C.

aj.crawford244@uniandes.edu.co

Mauricio S.

om.santos@uniandes.edu.co

Descriptive stats

Mean & Median

Sample mean: \[ \overline{x} = \frac{1}{n}\sum^{n}_{i=1}x_{i} \]

You can create the function:

new_mean <- function(x) {
  sum(x) / length(x)
}

new_mean(penguins$year)

[1] 2008.029

Or simply use a predefined mean:

mean(penguins$year, na.rm = TRUE)

[1] 2008.029

Sample median: \[ median= \begin{cases} x_{(n+1)/2} &\text{if $n \equiv 1$} \\ \frac{(x_{n/2} + x_{((n/2)+1)})}{2} &\text{if $n \equiv 0$} \end{cases} \]

In R a freshly defined function:

new_median <- function(x) {
  if (length(x) %% 2 != 0) {
    sort(x)[ceiling(length(x) / 2)]
  } else {
    (sort(x)[length(x) / 2] + sort(x)[(length(x) / 2) + 1]) / 2
  }
}

1: The expression length(x) %% 2 != 0 checks whether the sample size is odd (impar). The modulus operator %% returns the remainder of length(x) divided by 2; if the remainder is 1 (non-zero), the condition is TRUE and the function uses the odd-case formula.
2: Equation for n if it is odd (impar)
3: Equation for n if it is even (par)

new_median(penguins$body_mass_g)

[1] 4050

Or the predefined function

median(penguins$body_mass_g, na.rm = TRUE)

[1] 4050

Variance, Standard deviation & Variation coefficient

Sample variance (unbiased): \[ S^{2} = \frac{1}{n-1}\sum^{n}_{i=1}(x_{i}-\overline{x})^{2} \]

var(penguins$body_mass_g, na.rm = TRUE)

[1] 643131.1

Standard deviation

\[ S = \sqrt{\frac{1}{n-1}\sum^{n}_{i=1}(x_{i}-\overline{x})^{2}} \]

sd(penguins$body_mass_g, na.rm = TRUE)

[1] 801.9545

Variation coefficient

\[ CV = \frac{S}{\overline{x}} \times 100 \]

cv <- function(x, na.rm = TRUE) {
  (sd(x, na.rm = TRUE) / mean(x, na.rm = TRUE)) * 100
}

cv(penguins$body_mass_g, na.rm = TRUE)

[1] 19.08618

Confidence intervals

Estimates the range within which a population parameter is likely to fall. It provides a way to express the uncertainty or margin of error associated with a sample estimate. \[ \text{IC} = \bar{x} \pm Z \left( \frac{\sigma}{\sqrt{n}} \right) \]

Or if the population standard deviation of the population is unknown:

\[ \text{IC} = \bar{x} \pm t \left( \frac{s}{\sqrt{n}} \right) \]

Using `dplyr` for summarizing stats

library(dplyr)

penguins |>
  group_by(species)

penguins |>
  group_by(species) |>
  summarise(
    mean_body_mass_g = mean(body_mass_g, na.rm = TRUE)
  )

penguins |>
  group_by(species) |>
  summarise(
    mean_body_mass_g = mean(body_mass_g, na.rm = TRUE),
    variance_body_mass_g = var(body_mass_g, na.rm = TRUE)
  )

penguins |>
  group_by(species) |>
  summarise(
    mean_body_mass_g = mean(body_mass_g, na.rm = TRUE),
    variance_body_mass_g = var(body_mass_g, na.rm = TRUE),
    std_dev_body_mass_g = sd(body_mass_g, na.rm = TRUE)
  )

penguins |>
  group_by(species) |>
  summarise(
    mean_body_mass_g = mean(body_mass_g, na.rm = TRUE),
    variance_body_mass_g = var(body_mass_g, na.rm = TRUE),
    std_dev_body_mass_g = sd(body_mass_g, na.rm = TRUE),
    cv_body_mass_g = cv(body_mass_g, na.rm = TRUE)
  )

How to compute all summary statistics for all numeric variables in a dataset?

Solution in the next slide, but before take your time, breath and go back to previous slide…

allsummaries <- penguins |>
  summarise(
    .by = species,
    across(where(is.numeric),
      list(
        mean_calc = \(x) (mean(x, na.rm = TRUE)),
        median_calc = \(x) (median(x, na.rm = TRUE)),
        sd_calc = \(x) (sd(x, na.rm = TRUE)),
        cv_calc = \(x) (cv(x, na.rm = TRUE))
      ),
      .names = "{.fn}_{.col}"
    )
  )

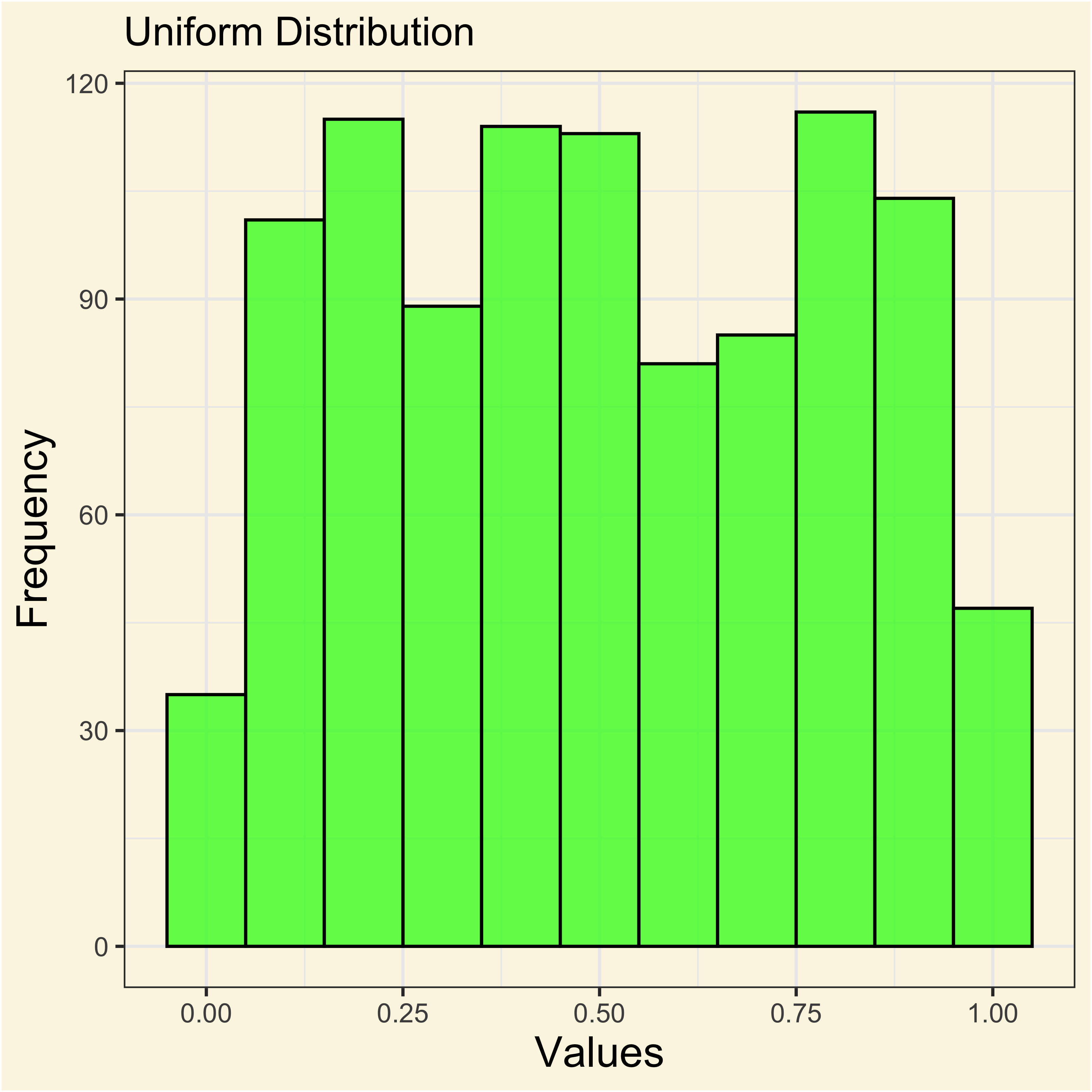
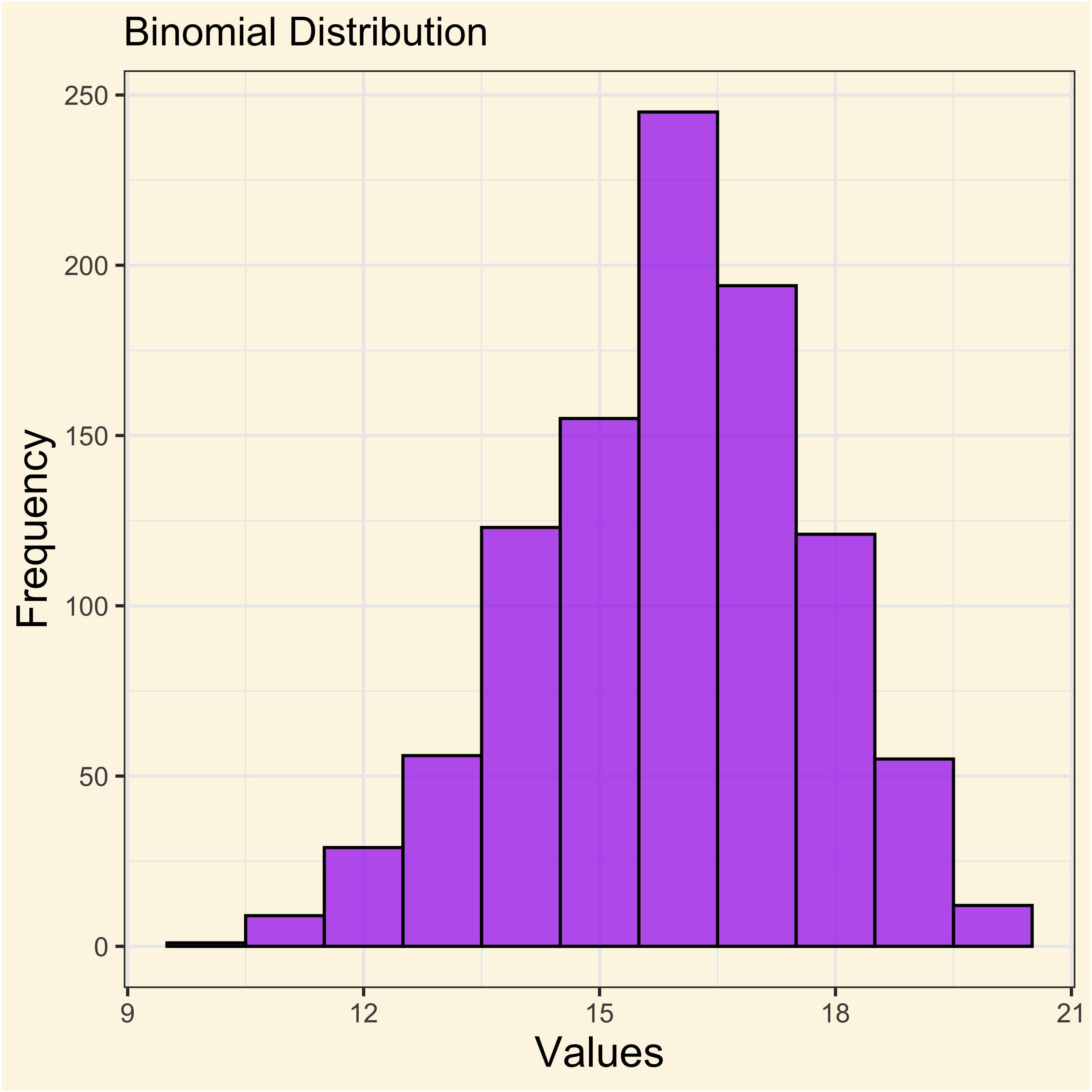
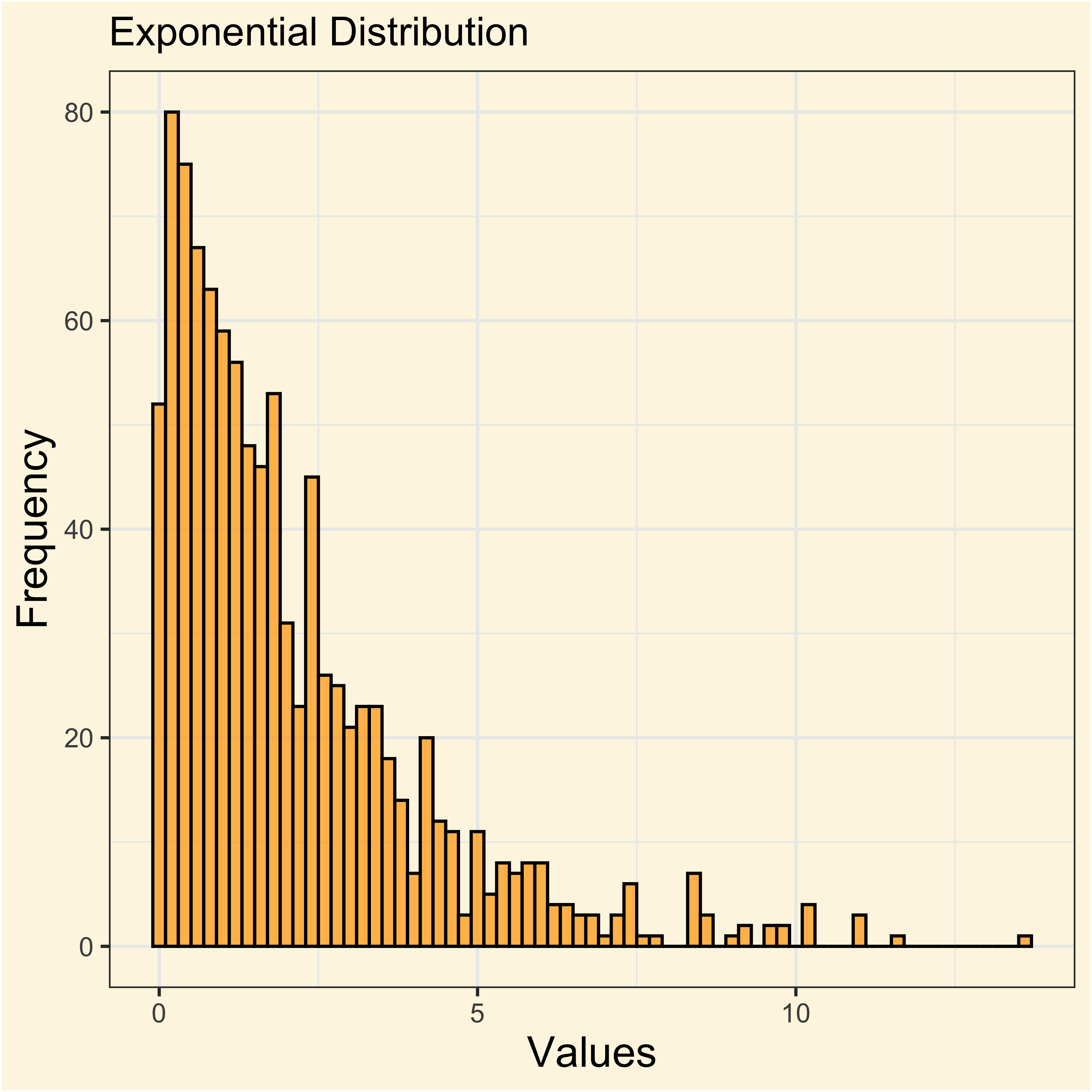
Distributions

dfuniform <- runif(1000, min = 0, max = 1)

ggplot(data.frame(x = dfuniform), aes(x)) +
  geom_histogram(
    binwidth = 0.1,
    fill = "green",
    color = "black",
    alpha = 0.7
  ) +
  labs(
    title = "Uniform Distribution",
    x = "Values",
    y = "Frequency"
  )

dfbin <- rbinom(1000, size = 20, prob = 0.8)

ggplot(data.frame(x = dfbin), aes(x)) +
  geom_histogram(
    binwidth = 1,
    fill = "purple",
    color = "black",
    alpha = 0.7
  ) +
  labs(
    title = "Binomial Distribution",
    x = "Values",
    y = "Frequency"
  )

dfexp <- rexp(1000, rate = 0.5)

ggplot(data.frame(x = dfexp), aes(x)) +
  geom_histogram(
    binwidth = 0.2,
    fill = "orange",
    color = "black",
    alpha = 0.7
  ) +
  labs(
    title = "Exponential Distribution",
    x = "Values",
    y = "Frequency"
  )

dfnormal <- rnorm(1000, mean = 0, sd = 1)

ggplot(data.frame(x = dfnormal), aes(x)) +
  geom_histogram(
    binwidth = 0.2,
    fill = "blue",
    color = "black",
    alpha = 0.7
  ) +
  labs(
    title = "Normal Distribution",
    x = "Values",
    y = "Frequency"
  )

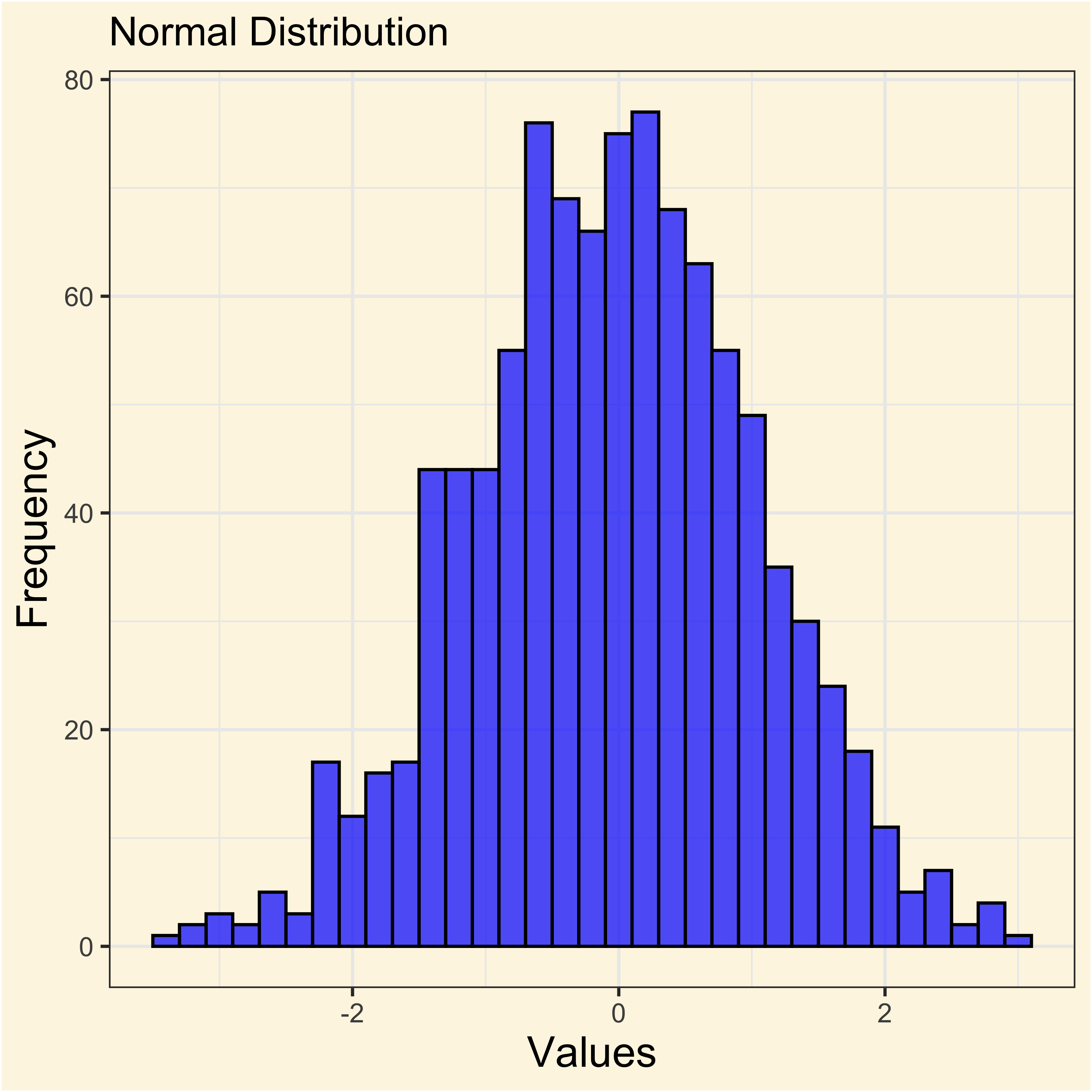
The standard normal distribution

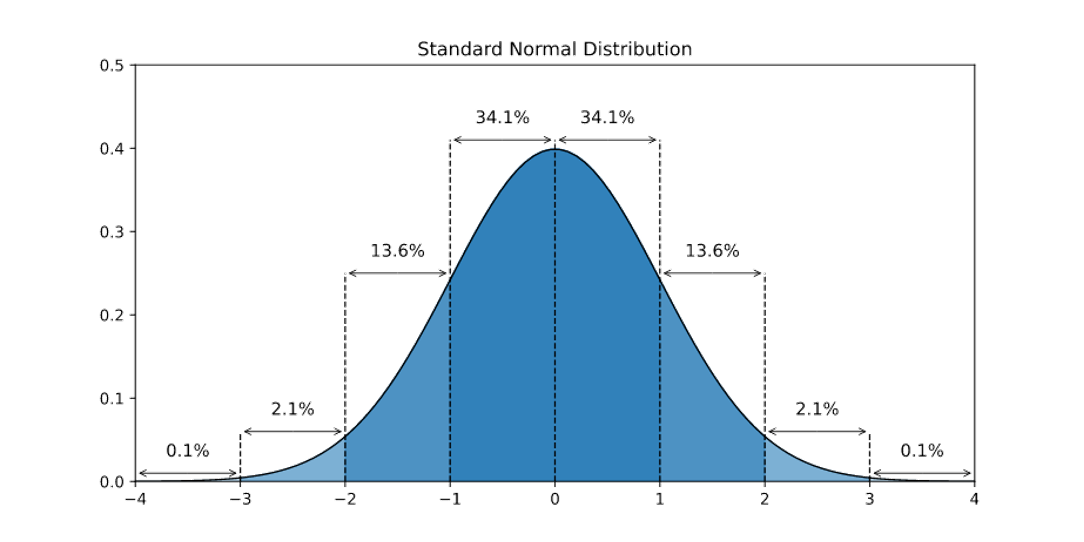
Where $z = \frac{x - \mu} {\sigma}$ is the standardization function, the result is that $\sigma = 1$ and $\mu = 0$

family of normality functions in `R`

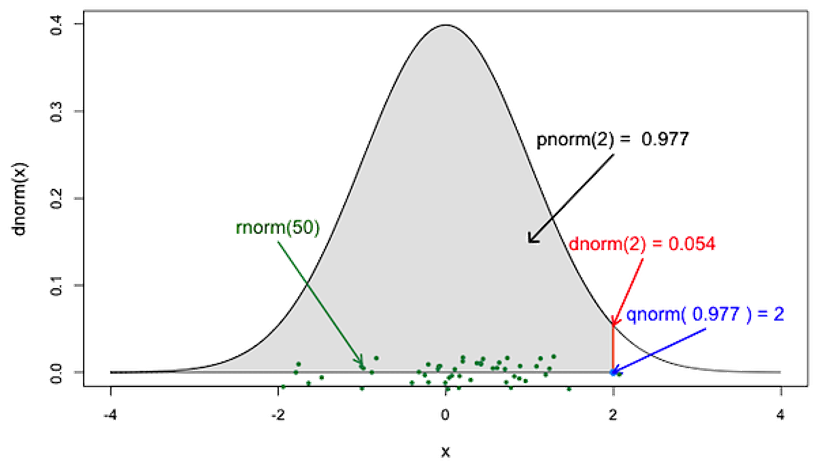
rnorm() generates pseudorandom normal numbers.
dnorm() is the probability density function (PDF)
pnorm() is the cumulative density function
qnorm() calculates the quantile of the normal distribution

Let’s try with an example:

Now, the Adelie penguins display an average bill length of 38.8 mm and its standard variation is 2.6 mm. What’s the percentage of penguins of 40 mm or smaller?

pnorm(40, mean = 38.8, sd = 2.6)

[1] 0.6777938

When the frequencies of a random variable $X$ cluster around a central value, it is said that it follows a normal distribution.

In summary a variable that appears to follow a normal distribution displays three properties:

Most values clustered around the average.
Extreme values are less frequent, but not impossibles.
Distribution display are quite symmetric from the mean.