Parametric & Non-Parametric tests

https://bit.ly/3V7CMsZ

Camilo G.
ca.garcia2@uniandes.edu.co
Alejandra S.
m.soto2@uniandes.edu.co
Ronald D.
r.diazf@uniandes.edu.co
Andrew C.
aj.crawford244@uniandes.edu.co
Mauricio S.
om.santos@uniandes.edu.co

How do we test whether two samples are different?

Do male penguins display greater body sizes than female?

adelie_penguins <- penguins |>
  filter(species == "Adelie") |>
  drop_na()

ggplot(adelie_penguins, aes(x = sex, y = body_mass_g, fill = sex)) +
  geom_boxplot(alpha = 0.5) +
  geom_jitter(width = 0.2) +
  labs(
    y = "Body mass (g)",
    x = ""
  )

Let’s try to test the resulting hypotheses:

Null hypothesis: \[H_{0}: \mu_{1} = \mu_{2}\] No variation between means

Alternative hypothesis: \[H_{A}: \mu_{1} \neq \mu_{2}\] Variation between means

Let’s make some important assumptions

  1. The two samples are independent.
  2. Variables display normal distribution.
  3. The two samples display equal variances.

Then,

And,

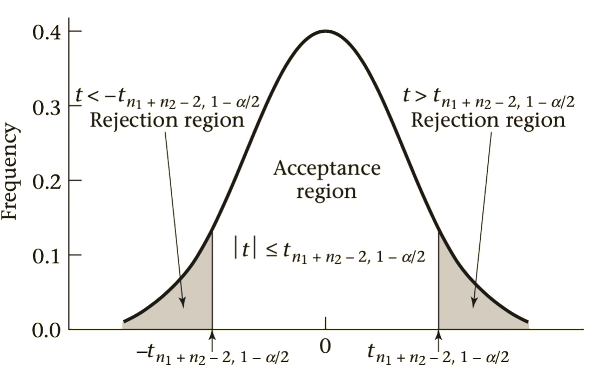
The T Distribution

\[ \bar{X}_{1} - \bar{X}_{2} \sim N\Bigg[\mu_{1} - \mu_{2},s^{2}\bigg(\frac{1}{n_{1}}+\frac{1}{n_{2}}\bigg)\Bigg] \]

If \(H_{0}\) is true \(\rightarrow\) \(\mu_{1} - \mu_{2} = 0\), then

\[ \bar{X}_{1} - \bar{X}_{2} \sim N\Bigg[0,s^{2}\bigg(\frac{1}{n_{1}}+\frac{1}{n_{2}}\bigg)\Bigg] \]

\[ \frac{\bar{X}_{1} - \bar{X}_{2}}{s\sqrt{\frac{1}{n_{1}}+\frac{1}{n_{2}}}} \sim N(0,1) \]

\[ \frac{\bar{X}_{1} - \bar{X}_{2}}{s\sqrt{\frac{1}{n_{1}}+\frac{1}{n_{2}}}} = t \]

Testing the hypothesis in R

The parametric T-test

A way to test the hypothesis is using the t.test() function:

t.test(body_mass_g ~ sex, adelie_penguins)

    Welch Two Sample t-test

data:  body_mass_g by sex
t = -13.126, df = 135.69, p-value < 2.2e-16
alternative hypothesis: true difference in means between group female and group male is not equal to 0
95 percent confidence interval:
 -776.3012 -573.0139
sample estimates:
mean in group female   mean in group male 
            3368.836             4043.493

Another alternative is to use the statsExpressions library:

library(statsExpressions)

adelie_ttest_table <- two_sample_test(
  data = adelie_penguins,
  x = sex,
  y = body_mass_g,
  type = "p",
  paired = FALSE
)

adelie_ttest_table

Adding stats to the barplot!

ggplot(
  adelie_penguins,
  aes(
    x = sex,
    y = body_mass_g,
    fill = sex
  )
) +
  geom_boxplot(alpha = 0.5) +
  geom_jitter(width = 0.2) +
  labs(
    y = "Body mass (g)",
    x = "",
    subtitle = parse(
      text = adelie_ttest_table$expression
    )
  )

From Indrajeet Patil1

Adding comparisons to the plot using ggsignif library!

ggplot(
  adelie_penguins,
  aes(
    x = sex,
    y = body_mass_g,
    fill = sex
  )
) +
  geom_boxplot(alpha = 0.5) +
  geom_jitter(width = 0.2) +
  labs(
    y = "Body mass (g)",
    x = "",
    subtitle = parse(
      text = adelie_ttest_table$expression
    )
  ) +
  geom_signif(
    comparisons = list(c("female", "male")),
    test = "t.test",
    map_signif_level = TRUE
  )

The non-parametric Mann-Whitney/Wilcox test

Let’s make some important assumptions

  1. The two samples are independent.
  2. Variables could display non-normal distribution.
  3. The two samples could display different variances (and sample sizes).

A way to test the hypothesis is using the wilkox.test() function:

wilcox.test(body_mass_g ~ sex, adelie_penguins, paired = FALSE)

    Wilcoxon rank sum test with continuity correction

data:  body_mass_g by sex
W = 310.5, p-value < 2.2e-16
alternative hypothesis: true location shift is not equal to 0

Another alternative is to use the statsExpressions library:

library(statsExpressions)

adelie_wilcox_table <- two_sample_test(
  data = adelie_penguins,
  x = sex,
  y = body_mass_g,
  type = "np",
  paired = FALSE
)

adelie_wilcox_table

Adding stats to the barplot!

ggplot(
  adelie_penguins,
  aes(
    x = sex,
    y = body_mass_g,
    fill = sex
  )
) +
  geom_boxplot(alpha = 0.5) +
  geom_jitter(width = 0.2) +
  labs(
    y = "Body mass (g)",
    x = "",
    subtitle = parse(
      text = adelie_wilcox_table$expression
    )
  )

Adding comparisons to the plot using ggsignif library!

ggplot(
  adelie_penguins,
  aes(
    x = sex,
    y = body_mass_g,
    fill = sex
  )
) +
  geom_boxplot(alpha = 0.5) +
  geom_jitter(width = 0.2) +
  labs(
    y = "Body mass (g)",
    x = "",
    subtitle = parse(
      text = adelie_wilcox_table$expression
    )
  ) +
  geom_signif(
    comparisons = list(c("female", "male")),
    test = "wilcox.test",
    map_signif_level = TRUE
  )