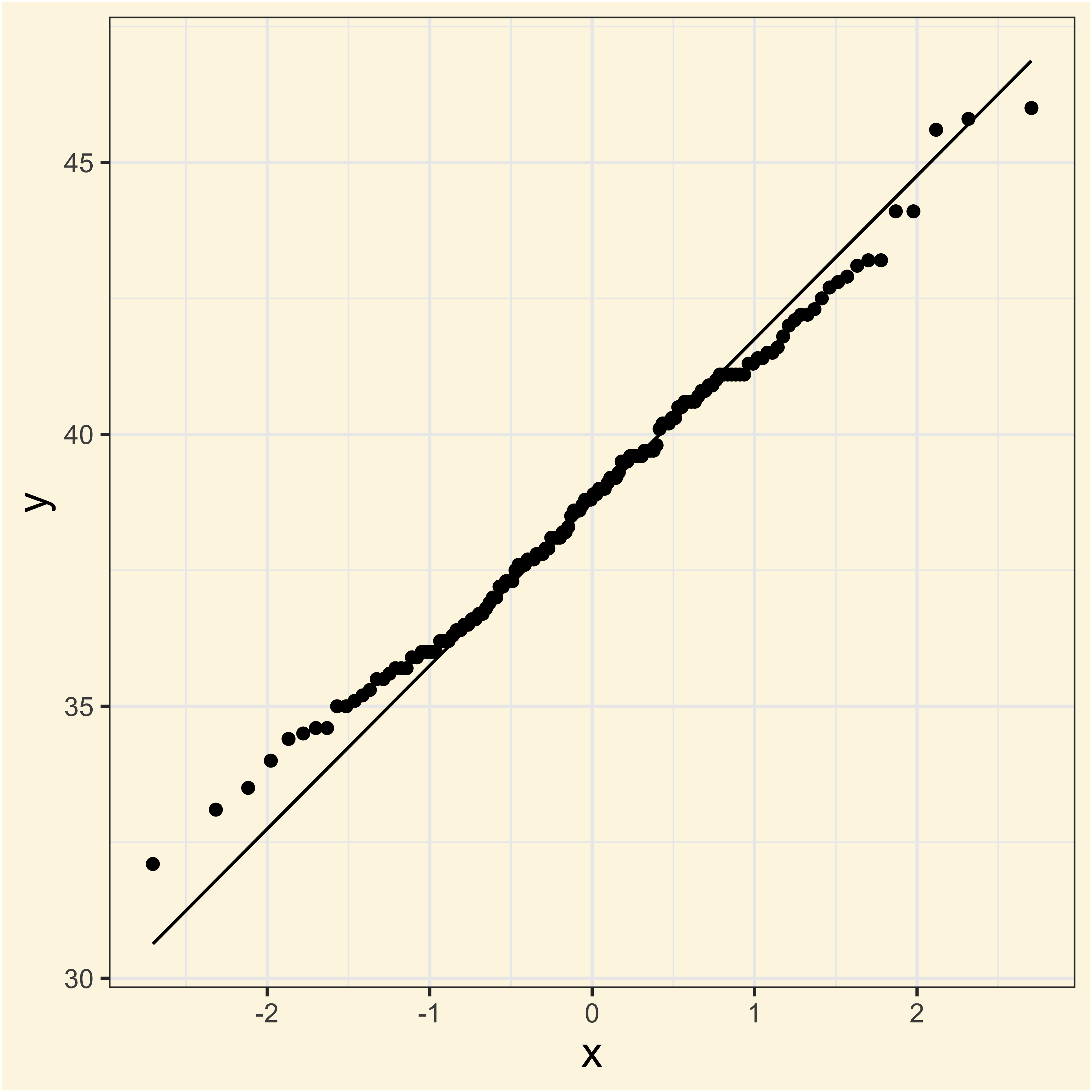
ggplot(adelie, aes(sample = bill_length_mm)) +
geom_qq() +
geom_qq_line()Normality and Transformations
https://bit.ly/41MCWbv
Camilo G.
Alejandra S.
Ronald D.
Andrew C.
Mauricio S.
What is normality?
When the frequencies of a random variable \(X\) cluster around a central value, it is said that it follows a normal distribution.
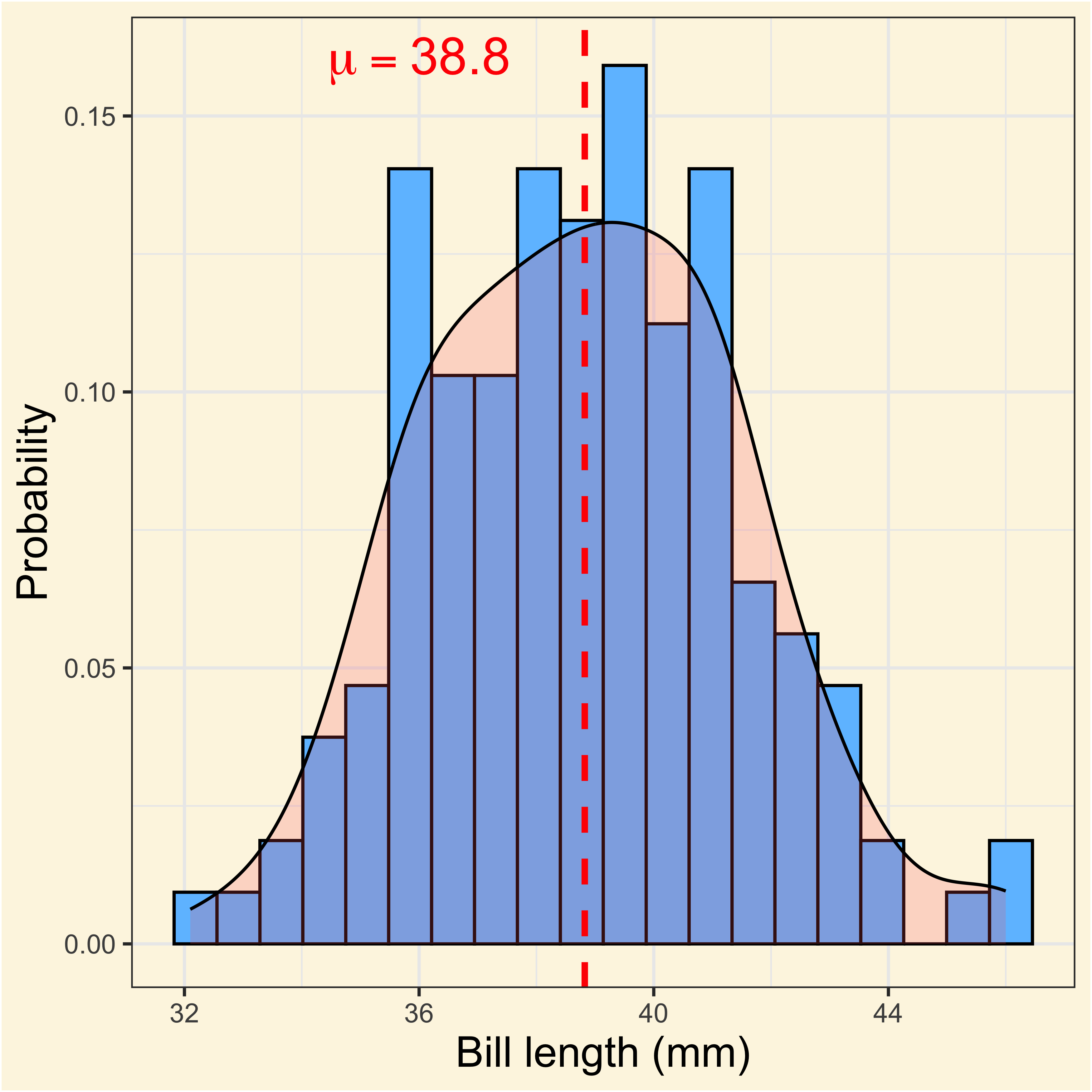
In summary a data set variable that appears to follow a normal distribution display three properties:
- Most values clustered around the average.
- Extreme values are less frequent, but not impossibles.
- Distribution display are quite symmetric from the mean.
Normality assessment
The Q-Q plot
Is my data really normal? Let’s see the quntile-quantile (Q-Q) plot:
The Shapiro-Wilk normality test:
In the Shapiro-Wilk normality test, normality is the null hypothesis. The alternative is that data do not follow a normal distribution. Therefore, if \(p\)-value \(\geq \alpha\) there is no evidence against normality.
shapiro.test(adelie$bill_length_mm)
Shapiro-Wilk normality test
data: adelie$bill_length_mm
W = 0.99289, p-value = 0.6848Transformations
The Log-Normal distribution
By applying a log transformation to a log-normal distribution, we can go back to a normal distribution
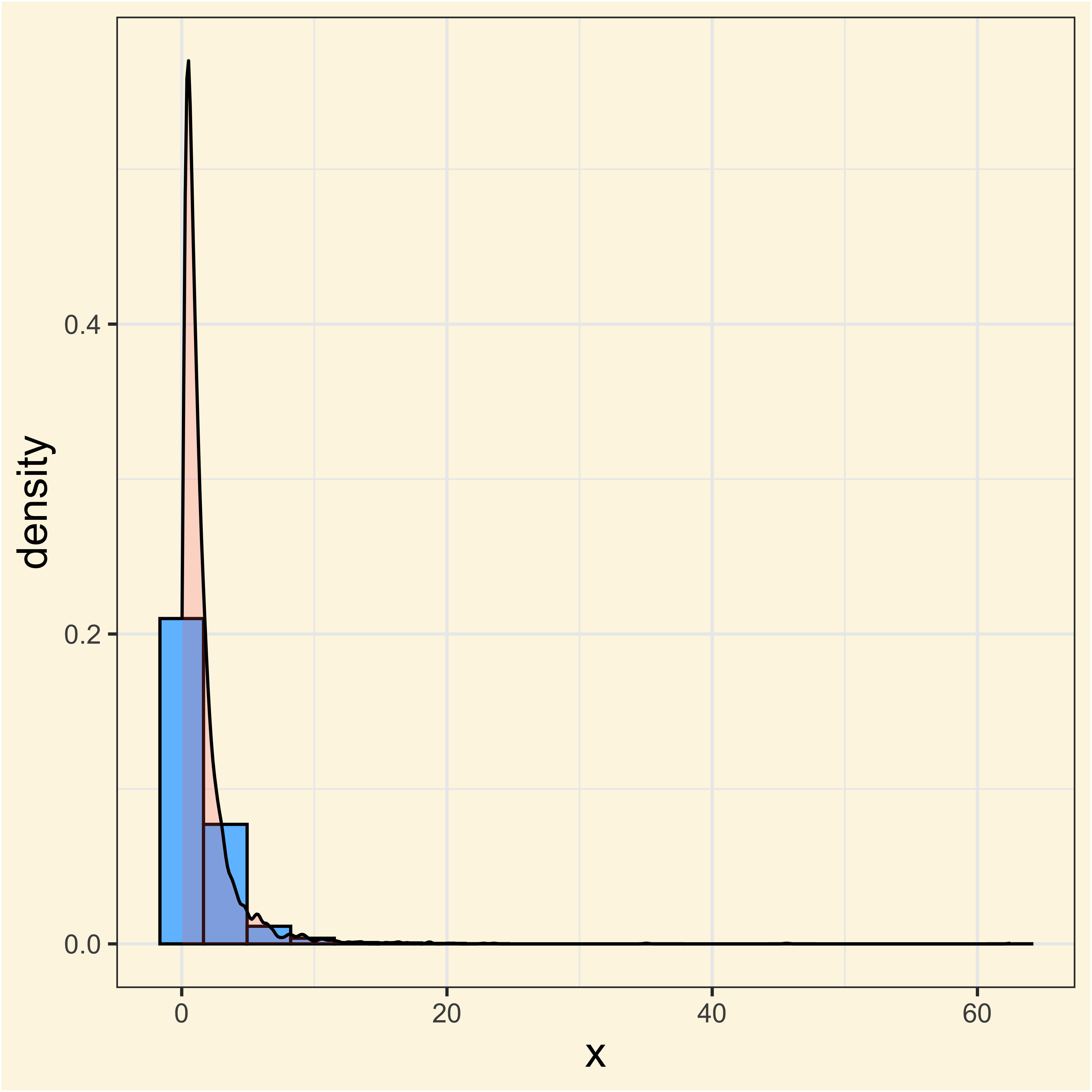
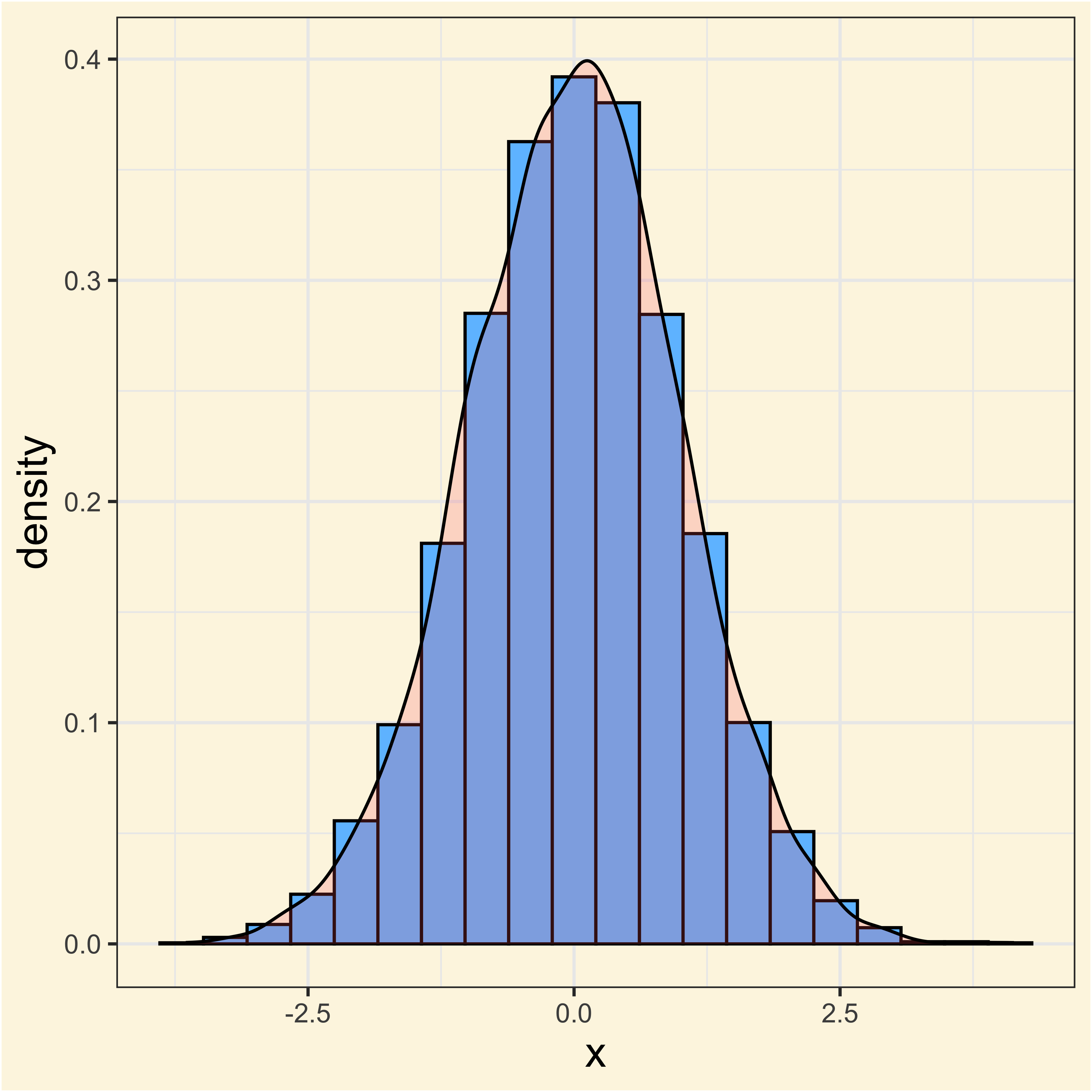
Other transformations
| Transformation | Function | R command | Use |
|---|---|---|---|
| Logarithmic to the right | \(x'=\ln{(x)}\) | log(x) |
Proportions or skewed to the right |
| Arcosin | \(x'=\arcsin{(\sqrt{x})}\) | asin(sqrt(x)) |
Proportions or percentages |
| Square root | \(x'=\sqrt{x+\frac{1}{2}}\) | sqrt(x+1/2) |
Counts |
| Exponential | \(x'=e^{x}\) | exp(x) |
skewed to the left |
| Reciprocal | \(x=\frac{1}{x}\) | 1/x |
skewed to the right |
Informative plots
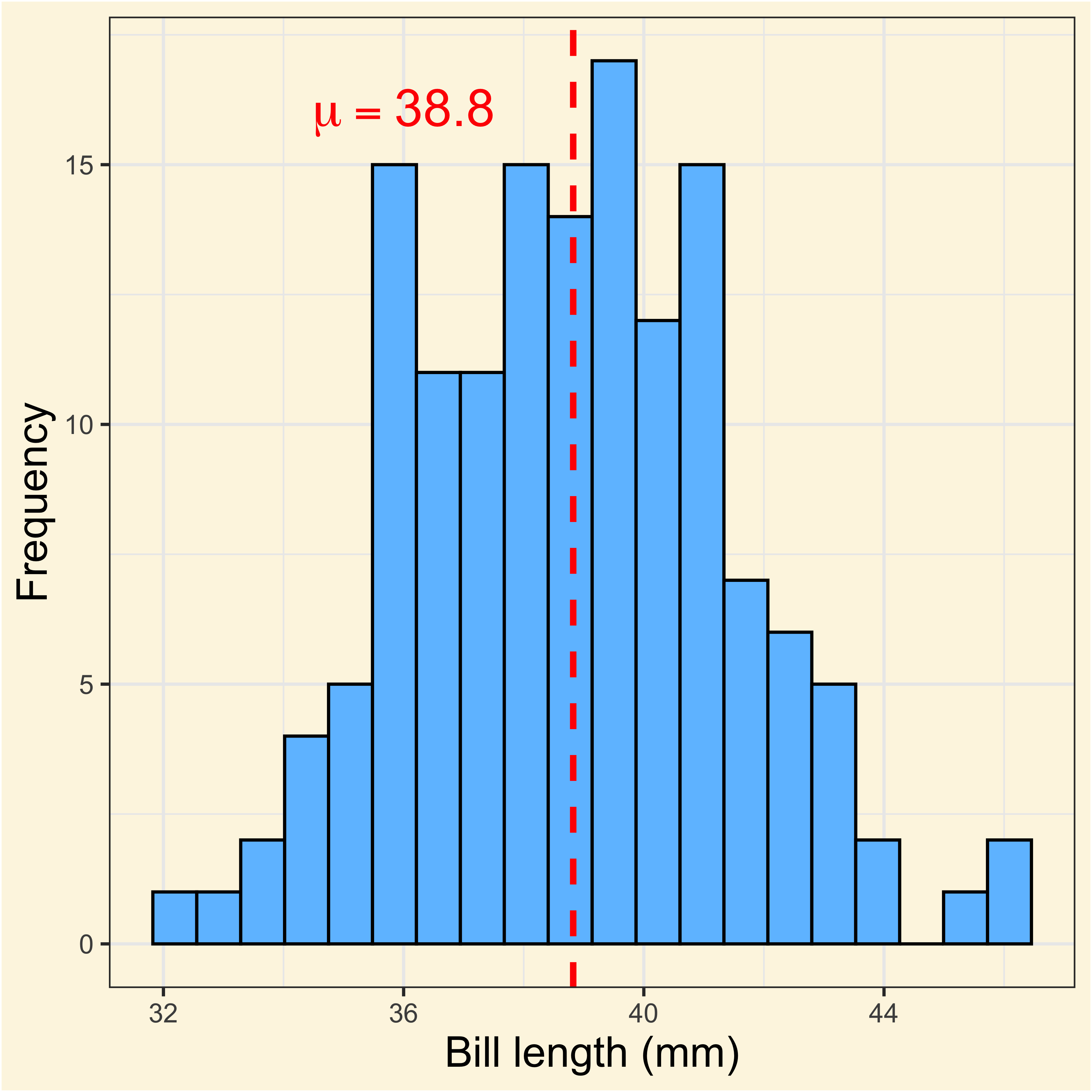
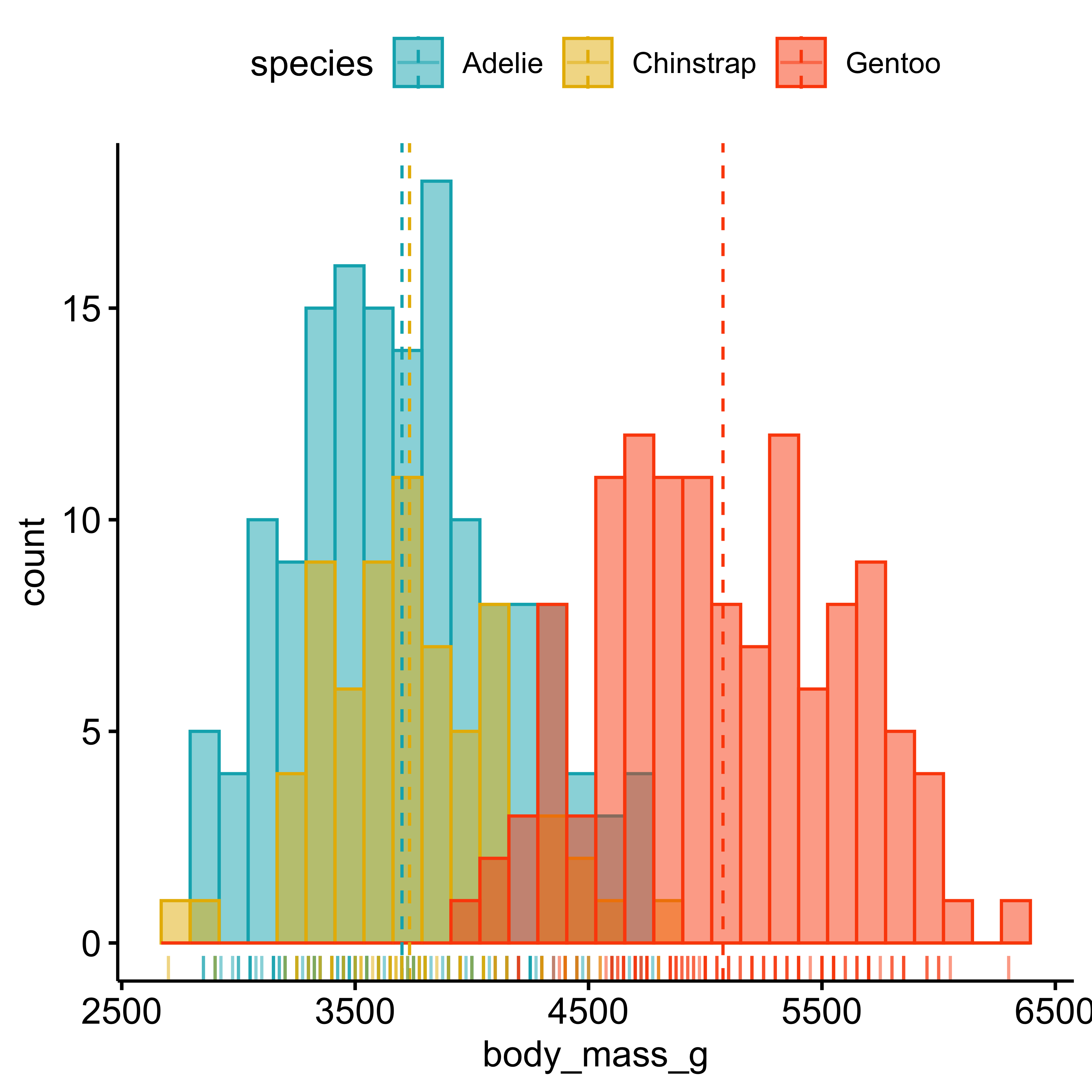
Histograms
gghistogram(penguins,
x = "body_mass_g",
add = "mean",
rug = TRUE,
color = "species",
fill = "species",
palette = c(
"#00AFBB",
"#E7B800",
"#FC4E07"
)
)
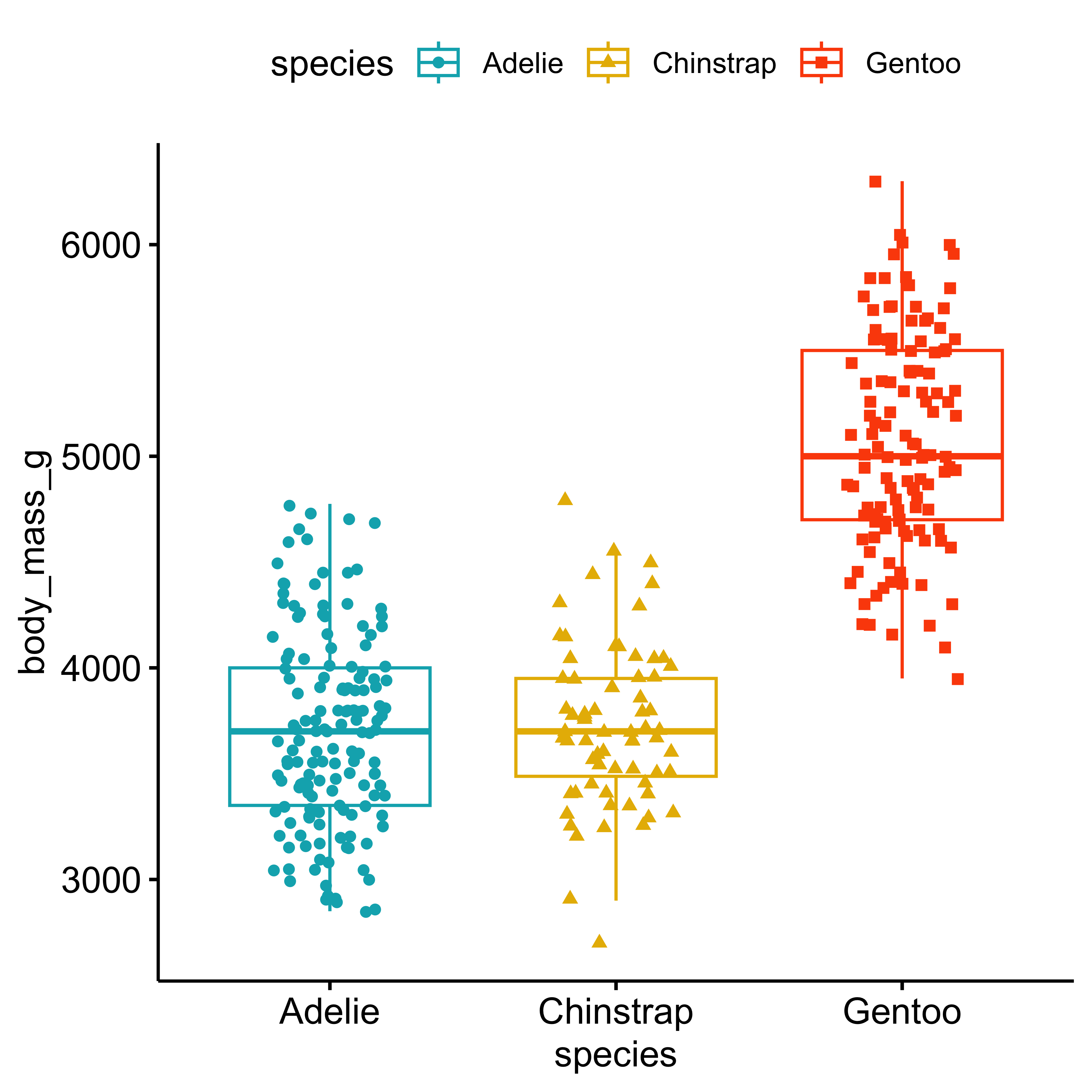
Box and Violin plots
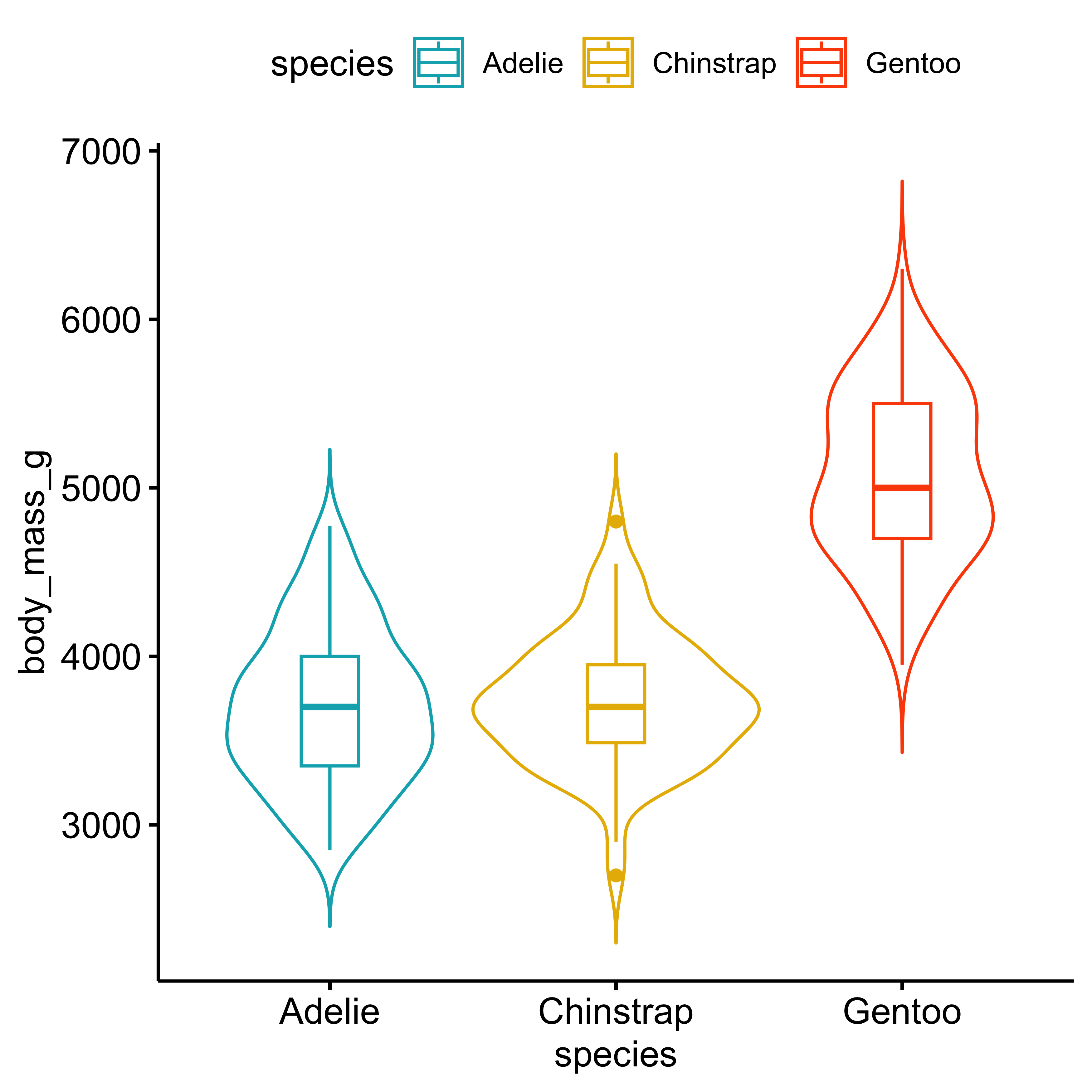
Violin plots (with stats)
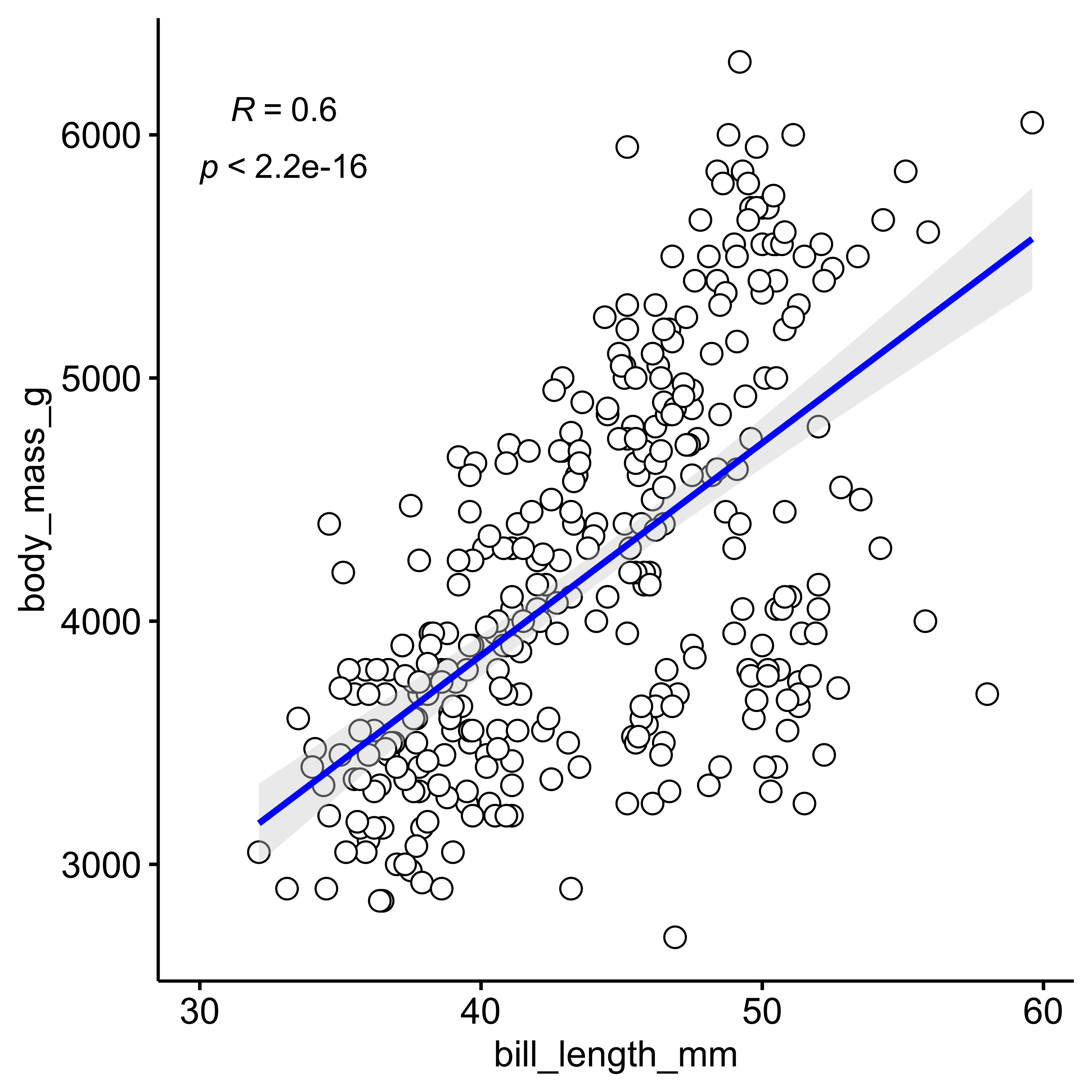
Scatter plot
BIOL2205 - Inferencia e Informática - DCB - Uniandes