Scoring ORFs

The ORF type is designed to be flexible and can store various types of information about ORFs through its features field. Since ORFCollection provides access to the underlying sequences, any method that can be applied to a BioSequence can be applied to extracted ORF sequences.

For instance, the lors function from the BioMarkovChains.jl package can be used to calculate a log-odds ratio score for ORF sequences.

Example: Scoring ORFs in the φX174 Genome

using BioSequences, GeneFinder

phi = dna"GTGTGAGGTTATAACGCCGAAGCGGTAAAAATTTTAATTTTTGCCGCTGAGGGGTTGACCAAGCGAAGCGCGGTAGGTTTTCTGCTTAGGAGTTTAATCATGTTTCAGACTTTTATTTCTCGCCATAATTCAAACTTTTTTTCTGATAAGCTGGTTCTCACTTCTGTTACTCCAGCTTCTTCGGCACCTGTTTTACAGACACCTAAAGCTACATCGTCAACGTTATATTTTGATAGTTTGACGGTTAATGCTGGTAATGGTGGTTTTCTTCATTGCATTCAGATGGATACATCTGTCAACGCCGCTAATCAGGTTGTTTCTGTTGGTGCTGATATTGCTTTTGATGCCGACCCTAAATTTTTTGCCTGTTTGGTTCGCTTTGAGTCTTCTTCGGTTCCGACTACCCTCCCGACTGCCTATGATGTTTATCCTTTGAATGGTCGCCATGATGGTGGTTATTATACCGTCAAGGACTGTGTGACTATTGACGTCCTTCCCCGTACGCCGGGCAATAACGTTTATGTTGGTTTCATGGTTTGGTCTAACTTTACCGCTACTAAATGCCGCGGATTGGTTTCGCTGAATCAGGTTATTAAAGAGATTATTTGTCTCCAGCCACTTAAGTGAGGTGATTTATGTTTGGTGCTATTGCTGGCGGTATTGCTTCTGCTCTTGCTGGTGGCGCCATGTCTAAATTGTTTGGAGGCGGTCAAAAAGCCGCCTCCGGTGGCATTCAAGGTGATGTGCTTGCTACCGATAACAATACTGTAGGCATGGGTGATGCTGGTATTAAATCTGCCATTCAAGGCTCTAATGTTCCTAACCCTGATGAGGCCGCCCCTAGTTTTGTTTCTGGTGCTATGGCTAAAGCTGGTAAAGGACTTCTTGAAGGTACGTTGCAGGCTGGCACTTCTGCCGTTTCTGATAAGTTGCTTGATTTGGTTGGACTTGGTGGCAAGTCTGCCGCTGATAAAGGAAAGGATACTCGTGATTATCTTGCTGCTGCATTTCCTGAGCTTAATGCTTGGGAGCGTGCTGGTGCTGATGCTTCCTCTGCTGGTATGGTTGACGCCGGATTTGAGAATCAAAAAGAGCTTACTAAAATGCAACTGGACAATCAGAAAGAGATTGCCGAGATGCAAAATGAGACTCAAAAAGAGATTGCTGGCATTCAGTCGGCGACTTCACGCCAGAATACGAAAGACCAGGTATATGCACAAAATGAGATGCTTGCTTATCAACAGAAGGAGTCTACTGCTCGCGTTGCGTCTATTATGGAAAACACCAATCTTTCCAAGCAACAGCAGGTTTCCGAGATTATGCGCCAAATGCTTACTCAAGCTCAAACGGCTGGTCAGTATTTTACCAATGACCAAATCAAAGAAATGACTCGCAAGGTTAGTGCTGAGGTTGACTTAGTTCATCAGCAAACGCAGAATCAGCGGTATGGCTCTTCTCATATTGGCGCTACTGCAAAGGATATTTCTAATGTCGTCACTGATGCTGCTTCTGGTGTGGTTGATATTTTTCATGGTATTGATAAAGCTGTTGCCGATACTTGGAACAATTTCTGGAAAGACGGTAAAGCTGATGGTATTGGCTCTAATTTGTCTAGGAAATAACCGTCAGGATTGACACCCTCCCAATTGTATGTTTTCATGCCTCCAAATCTTGGAGGCTTTTTTATGGTTCGTTCTTATTACCCTTCTGAATGTCACGCTGATTATTTTGACTTTGAGCGTATCGAGGCTCTTAAACCTGCTATTGAGGCTTGTGGCATTTCTACTCTTTCTCAATCCCCAATGCTTGGCTTCCATAAGCAGATGGATAACCGCATCAAGCTCTTGGAAGAGATTCTGTCTTTTCGTATGCAGGGCGTTGAGTTCGATAATGGTGATATGTATGTTGACGGCCATAAGGCTGCTTCTGACGTTCGTGATGAGTTTGTATCTGTTACTGAGAAGTTAATGGATGAATTGGCACAATGCTACAATGTGCTCCCCCAACTTGATATTAATAACACTATAGACCACCGCCCCGAAGGGGACGAAAAATGGTTTTTAGAGAACGAGAAGACGGTTACGCAGTTTTGCCGCAAGCTGGCTGCTGAACGCCCTCTTAAGGATATTCGCGATGAGTATAATTACCCCAAAAAGAAAGGTATTAAGGATGAGTGTTCAAGATTGCTGGAGGCCTCCACTATGAAATCGCGTAGAGGCTTTGCTATTCAGCGTTTGATGAATGCAATGCGACAGGCTCATGCTGATGGTTGGTTTATCGTTTTTGACACTCTCACGTTGGCTGACGACCGATTAGAGGCGTTTTATGATAATCCCAATGCTTTGCGTGACTATTTTCGTGATATTGGTCGTATGGTTCTTGCTGCCGAGGGTCGCAAGGCTAATGATTCACACGCCGACTGCTATCAGTATTTTTGTGTGCCTGAGTATGGTACAGCTAATGGCCGTCTTCATTTCCATGCGGTGCACTTTATGCGGACACTTCCTACAGGTAGCGTTGACCCTAATTTTGGTCGTCGGGTACGCAATCGCCGCCAGTTAAATAGCTTGCAAAATACGTGGCCTTATGGTTACAGTATGCCCATCGCAGTTCGCTACACGCAGGACGCTTTTTCACGTTCTGGTTGGTTGTGGCCTGTTGATGCTAAAGGTGAGCCGCTTAAAGCTACCAGTTATATGGCTGTTGGTTTCTATGTGGCTAAATACGTTAACAAAAAGTCAGATATGGACCTTGCTGCTAAAGGTCTAGGAGCTAAAGAATGGAACAACTCACTAAAAACCAAGCTGTCGCTACTTCCCAAGAAGCTGTTCAGAATCAGAATGAGCCGCAACTTCGGGATGAAAATGCTCACAATGACAAATCTGTCCACGGAGTGCTTAATCCAACTTACCAAGCTGGGTTACGACGCGACGCCGTTCAACCAGATATTGAAGCAGAACGCAAAAAGAGAGATGAGATTGAGGCTGGGAAAAGTTACTGTAGCCGACGTTTTGGCGGCGCAACCTGTGACGACAAATCTGCTCAAATTTATGCGCGCTTCGATAAAAATGATTGGCGTATCCAACCTGCAGAGTTTTATCGCTTCCATGACGCAGAAGTTAACACTTTCGGATATTTCTGATGAGTCGAAAAATTATCTTGATAAAGCAGGAATTACTACTGCTTGTTTACGAATTAAATCGAAGTGGACTGCTGGCGGAAAATGAGAAAATTCGACCTATCCTTGCGCAGCTCGAGAAGCTCTTACTTTGCGACCTTTCGCCATCAACTAACGATTCTGTCAAAAACTGACGCGTTGGATGAGGAGAAGTGGCTTAATATGCTTGGCACGTTCGTCAAGGACTGGTTTAGATATGAGTCACATTTTGTTCATGGTAGAGATTCTCTTGTTGACATTTTAAAAGAGCGTGGATTACTATCTGAGTCCGATGCTGTTCAACCACTAATAGGTAAGAAATCATGAGTCAAGTTACTGAACAATCCGTACGTTTCCAGACCGCTTTGGCCTCTATTAAGCTCATTCAGGCTTCTGCCGTTTTGGATTTAACCGAAGATGATTTCGATTTTCTGACGAGTAACAAAGTTTGGATTGCTACTGACCGCTCTCGTGCTCGTCGCTGCGTTGAGGCTTGCGTTTATGGTACGCTGGACTTTGTGGGATACCCTCGCTTTCCTGCTCCTGTTGAGTTTATTGCTGCCGTCATTGCTTATTATGTTCATCCCGTCAACATTCAAACGGCCTGTCTCATCATGGAAGGCGCTGAATTTACGGAAAACATTATTAATGGCGTCGAGCGTCCGGTTAAAGCCGCTGAATTGTTCGCGTTTACCTTGCGTGTACGCGCAGGAAACACTGACGTTCTTACTGACGCAGAAGAAAACGTGCGTCAAAAATTACGTGCGGAAGGAGTGATGTAATGTCTAAAGGTAAAAAACGTTCTGGCGCTCGCCCTGGTCGTCCGCAGCCGTTGCGAGGTACTAAAGGCAAGCGTAAAGGCGCTCGTCTTTGGTATGTAGGTGGTCAACAATTTTAATTGCAGGGGCTTCGGCCCCTTACTTGAGGATAAATTATGTCTAATATTCAAACTGGCGCCGAGCGTATGCCGCATGACCTTTCCCATCTTGGCTTCCTTGCTGGTCAGATTGGTCGTCTTATTACCATTTCAACTACTCCGGTTATCGCTGGCGACTCCTTCGAGATGGACGCCGTTGGCGCTCTCCGTCTTTCTCCATTGCGTCGTGGCCTTGCTATTGACTCTACTGTAGACATTTTTACTTTTTATGTCCCTCATCGTCACGTTTATGGTGAACAGTGGATTAAGTTCATGAAGGATGGTGTTAATGCCACTCCTCTCCCGACTGTTAACACTACTGGTTATATTGACCATGCCGCTTTTCTTGGCACGATTAACCCTGATACCAATAAAATCCCTAAGCATTTGTTTCAGGGTTATTTGAATATCTATAACAACTATTTTAAAGCGCCGTGGATGCCTGACCGTACCGAGGCTAACCCTAATGAGCTTAATCAAGATGATGCTCGTTATGGTTTCCGTTGCTGCCATCTCAAAAACATTTGGACTGCTCCGCTTCCTCCTGAGACTGAGCTTTCTCGCCAAATGACGACTTCTACCACATCTATTGACATTATGGGTCTGCAAGCTGCTTATGCTAATTTGCATACTGACCAAGAACGTGATTACTTCATGCAGCGTTACCATGATGTTATTTCTTCATTTGGAGGTAAAACCTCTTATGACGCTGACAACCGTCCTTTACTTGTCATGCGCTCTAATCTCTGGGCATCTGGCTATGATGTTGATGGAACTGACCAAACGTCGTTAGGCCAGTTTTCTGGTCGTGTTCAACAGACCTATAAACATTCTGTGCCGCGTTTCTTTGTTCCTGAGCATGGCACTATGTTTACTCTTGCGCTTGTTCGTTTTCCGCCTACTGCGACTAAAGAGATTCAGTACCTTAACGCTAAAGGTGCTTTGACTTATACCGATATTGCTGGCGACCCTGTTTTGTATGGCAACTTGCCGCCGCGTGAAATTTCTATGAAGGATGTTTTCCGTTCTGGTGATTCGTCTAAGAAGTTTAAGATTGCTGAGGGTCAGTGGTATCGTTATGCGCCTTCGTATGTTTCTCCTGCTTATCACCTTCTTGAAGGCTTCCCATTCATTCAGGAACCGCCTTCTGGTGATTTGCAAGAACGCGTACTTATTCGCCACCATGATTATGACCAGTGTTTCCAGTCCGTTCAGTTGTTGCAGTGGAATAGTCAGGTTAAATTTAATGTGACCGTTTATCGCAATCTGCCGACCACTCGCGATTCAATCATGACTTCGTGATAAAAGATTGA"

collection = findorfs(phi, finder=NaiveFinder, minlen=75)

We can now calculate scores using the lors (log-odds ratio score) function from BioMarkovChains.jl:

using BioMarkovChains

# Extract sequences and calculate scores
orfseqs = [sequence(collection, i) for i in eachindex(collection)]
scores = lors.(orfseqs)

Understanding the Log-Odds Ratio Score

A sequence of DNA can be scored using a Markov model of the transition probabilities. The log-odds ratio score is defined as:

$$\begin{array}{r}S(x)=\sum _{i=1}^L{\beta }_{x_{i}x}=\sum _{i=1}\log \frac{a_{i-1}^{{\mathcal{m}}_1}{x}_i}{a_{i-1}^{{\mathcal{m}}_2}{x}_i}\end{array}$$

Where $a_{i-1}^{{\mathcal{m}}_1}{x}_i$ is the transition probability from state $x_{i-1}$ to $x_i$ in model 1 (coding), and $a_{i-1}^{{\mathcal{m}}_2}{x}_i$ is the same for model 2 (non-coding).

Visualizing ORF Scores

using FASTX, CairoMakie

# Read lambda genome
lambdaseq = open(FASTA.Reader, "test/data/NC_001416.1.fasta") do reader
    FASTX.sequence(LongDNA{4}, first(reader))
end

# Find ORFs and calculate scores
collection = findorfs(lambdaseq, finder=NaiveFinder, minlen=100)
orfseqs = [sequence(collection, i) for i in eachindex(collection)]

lambdascores = lors.(orfseqs)
lambdalengths = length.(orfseqs)

# Generate random sequences for comparison
randseqs = [randdnaseq(rand(100:2500)) for _ in 1:length(collection)]
randscores = lors.(randseqs)
randlengths = length.(randseqs)

# Plot comparison
f = Figure()
ax = Axis(f[1, 1], xlabel="Length", ylabel="Log-odds ratio (Bits)")

scatter!(ax, randlengths, randscores, marker=:circle, markersize=6, 
         color=:black, label="Random sequences")
scatter!(ax, lambdalengths, lambdascores, marker=:rect, markersize=6, 
         color=:blue, label="Lambda ORFs")

axislegend(ax)
f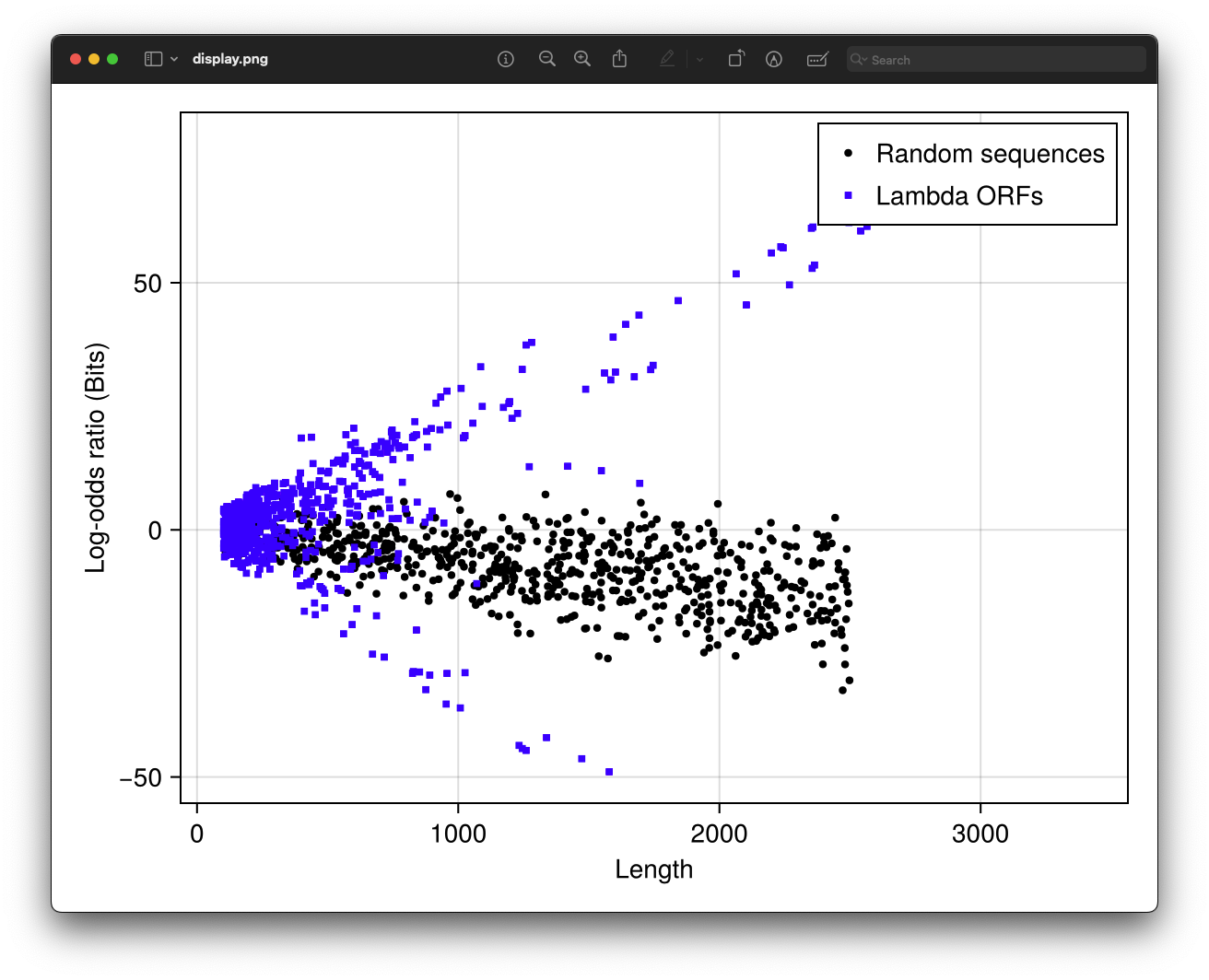

This plot shows that ORFs in the lambda genome have higher scores than random sequences, indicating they are more likely to be coding regions.